เซต
เซต เป็นคำที่ไม่ให้ให้นิยาม (Undefined Term) เรามักใช้เซตแทนสิ่งที่อยู่ร่วมกัน ซึ่งหมายถึงกลุ่มของสิ่งต่างๆ ที่เราสามารถกำหนดสมาชิกได้ชัดเจน (Well-Defined) หรือก็คือความหมายของเซตนั่นเอง
การเขียนเซต
1. เขียนแบบแจกแจงสมาชิก (Tabular Form) เป็นการเขียนเซตโดยบรรจุสมาชิกทั้งหมดของเซตลงในวงเล็บปีกกา และระหว่างสมาชิกแต่ละตัวคั่นด้วยเครื่องหมายจุลภาค (,)
เช่น {A,B,C} หรือ {1, 2, 3} เป็นต้น
(หมายเหตุ: ถ้าเซตมีจำนวนสมาชิกมากมาย เราใช้ “…” แทนสมาชิกที่เหลือ)
2. เขียนสับเซตแบบบอกเงื่อนไขของสมาชิกในสับเซต (Set builder form)
มีหลักการ คือ แทนสมาชิกของเซตด้วยตัวแปรแล้วกำหนดเงื่อนไขเกี่ยวกับตัวแปรนั้น เพื่อแสดงว่ามีสิ่งใดบ้างที่เป็นสมาชิกของเซต
วิธีเขียนเซตโดยวิธีนี้ คือ เขียนตัวแปรและสิ่งที่กำหนดเงื่อนไขเกี่ยวกับตัวแปรลงในวงเล็บปีกกาและคั้นตัวแปรกับสิ่งที่กำหนดเงื่อนไขเกี่ยวกับตัวแปรด้วยเครื่องหมาย “|” หรือ “:”
3. การเขียนเซตด้วยวิธีอื่นๆ เช่น แบบบรรยาย, แบบใช้แผนภาพเวนน์, แบบช่วง เป็นต้น
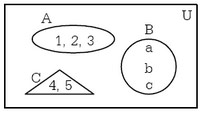
แผนภาพเวนน์-ออยเลอร์ เป็นแผนภาพที่ใช้เขียนแทนเซตซึ่งแทนเอกภพสัมพัทธ์ U ด้วยสี่เหลี่ยมผืนผ้า และแทนเซต A, B, … ด้วยรูปวงกลม หรือวงรี หรือรูปปิดอื่นๆ ดังรูป
รูปวงรี แทนเซต A โดยที่ A = {1, 2, 3}
รูปวงกลม แทนเซต B โดยที่ B = {a, b, c}
รูปสามเหลี่ยม แทนเซต C โดยที่ C = {4,5}
ซึ่งในเรื่องของแผนภาพนี้เรายังทำไปประยุกต์ใช้ในเรื่องการกระทำระหว่างเซต ซึ่งแสดงด้วยแผนภาพจะทำให้ดูเข้าใจง่ายขึ้น
เซตถูกจำแนกออกเป็นสองอย่างด้วยกันคือ เซตจำกัด และเซตอนันต์ ซึ่งจะมีวิธีแยกแยะเซตทั้งสองนี้ออกจากกัน เซตจำกัดคือเซตที่เราสามารถบอกจำนวนสมาชิกได้ ตรงกันข้ามกับเซตอนันต์
1. เซตจำกัด (Finite Set)
เซตจำกัด (Finite Set) คือ เซตที่สามารถนับจำนวนสมาชิกได้ทั้งหมดและมีจำนวนที่แน่นอน เช่น A = {1, 2, 3, … ,20} จะเห็นได้ว่าเซต A สามารถบอกจำนวนสมาชิกได้ว่าเซตนี้มีจำนวนสมาชิกทั้งหมด 20 ตัว ดังนั้น เซต A จึงเป็นเซตจำกัด
ลองดูอีกตัวอย่างกันนะครับ B = { 3 } จะเห็นได้ว่าเซต B สามารถที่จะบอกจำนวนสมาชิกได้ คือ 1 ตัว ดังนั้นเซต B จึงเป็นเซตจำกัด
**หมายเหตุ เซตว่าง (Empty Set) ถือเป็นเซตจำกัด เขียนสัญลักษณ์แทนเซตว่างได้ดังนี้ หรือ { }
2. เซตอนันต์ (Infinite Set)
เซตอนันต์ (Infinite Set) คือ เซตที่ไม่สามารถบอกจำนวนสมาชิกได้เพราะสมาชิกมีจำนวนมาก เช่น A = {1, 2, 3, … } จะเห็นได้ว่าเซต A ไม่สามารถบอกจำนวนสมาชิกตัวสุดท้ายที่อยู่ในเซตนี้ได้หมด ดังนั้นเซต A จึงเป็นเซตอนันต์
ลองมาดูกันอีกตัวอย่างนึง B = {3, 5, 7, …} จะเห็นได้ว่าเซต B ไม่สามารถบอกจำนวนสมาชิกที่เป็นจำนวนคี่ได้หมด ดังนั้นเซต B จึงเป็นเซตอนันต์
เซตว่าง และเอกภพสัมพัทธ์ จากบทเรียนเรื่องเซต คณิตศาสตร์ ม.4 ถือเป็นพื้นฐานของเรื่องเซต ที่เราควรจะทำความสนิทสนมกับมันให้มาก เพราะมันเป็นพื้นฐานทั้งหมดในการเรียนเรื่องเซต
เซตว่าง (Empty Set)
เซตว่าง คือ เซตที่ไม่มีสมาชิก หรือมีจำนวนสมาชิกในเซตเป็นศูนย์ สามารถเขียนแทนได้ด้วยสัญลักษณ์ {} หรือ Ø
ตัวอย่างเช่น
A = {x | x เป็นจำนวนเต็ม และ 1 < x < 2} ∴ A = Ø
B = { x | x เป็นจำนวนเต็มบวก และ x + 1 = 0 } ∴ B = Ø
เนื่องจากเราสามารถบอกจำนวนสมาชิกของเซตว่างได้ ดังนั้น เซตว่างเป็นเซตจำกัด
เอกภพสัมพัทธ์ (Relative Universe)
เอกภพสัมพัทธ์ คือ เซตที่กำหนดขอบเขตของสิ่งที่ต้องการศึกษา ซึ่งถือว่าเป็นเซตที่ใหญ่ที่สุด โดยมีข้อตกลงว่า ต่อไปจะกล่าวถึงสมาชิกของเซตนี้เท่านั้น จะไม่มีการกล่าวถึงสิ่งใดที่นอกเหนือไปจากสมาชิกของเซตที่กำหนดขึ้นนี้ โดยทั่วไปนิยมใช้สัญลักษณ์ U แทนเอกภพสัมพัทธ์
เช่น กำหนดให้ U = {1,2,3,4,5,6,7,8}
A = {1,3,5,7}
B = {2,4,8}
หรือกำหนดให้ U = {x ε I+ | 1<x<20}
A = {x ε U | x=n+3 เมื่อ n เป็นจำนสวนเต็มคี่บวก}
B = {x ε U | x=n+3 เมื่อ n เป็นจำนสวนเต็มคู่บวก}
นั่นคือทั้ง A และ B เป็นสับเซตของ U
ยูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต เป็นส่วนหนึ่งของการกระทำระหว่างเซต เรานิยมเขียนออกมาในสองรูปแบบด้วยกันคือแบบสมการ และแผนภาพเวนน์-ออยเลอร์ เราลองมาดูกันครับว่ายูเนียน อินเตอร์เซกชัน และคอมพลีเมนต์ของเซต เป็นอย่างไรพร้อมตัวอย่าง
ยูเนียน (Union)
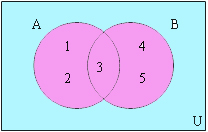
ยูเนียน (Union) มีนิยามว่า เซต A ยูเนียนกับเซต B คือเซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A หรือ เซต B หรือทั้ง A และ B สามารถเขียนแทนได้ด้วย สัญลักษณ์ A ∪ B
ตัวอย่างเช่น
A ={1,2,3}
B= {3,4,5}
∴ A ∪ B = {1,2,3,4,5}
เราสามารถเขียนการยูเนี่ยนลงในแผนภาพได้ดังนี้
อินเตอร์เซกชัน (Intersection)
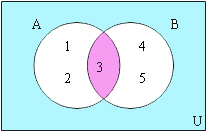
อินเตอร์เซกชัน (Intersection) มีนิยามคือ เซต A อินเตอร์เซกชันเซต B คือ เซตซึ่งประกอบด้วยสมาชิกที่เป็นสมาชิกของเซต A และเซต B สามารถเขียนแทนได้ด้วยสัญลักษณ์ A ∩ B
ตัวอย่างเช่น
A ={1,2,3}
B = {3,4,5}
∴ A ∩ B = {3}
เราสามารถเขียนการอินเตอร์เซกชันลงในแผนภาพได้ดังนี้
คอมพลีเมนต์ (Complements)
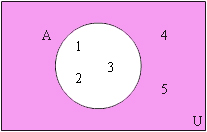
คอมพลีเมนต์ (Complements) มีนิยามคือ ถ้าเซต A ใดๆ ในเอกภพสัมพัทธ์ U แล้วคอมพลีเมนต์ของเซต A คือ เซตที่ประกอบด้วยสมาชิกที่เป็นสมาชิกของ U แต่ไม่เป็นสมาชิกของ A สามารถเขียนแทนได้ด้วยสัญลักษณ์ A’
ตัวอย่างเช่น
U = {1,2,3,4,5}
A ={1,2,3}
∴ A’ = {4,5}
เราสามารถเขียนการคอมพลีเมนต์ของเซตลงในแผนภาพได้ดังนี้
สับเซตและเพาเวอร์เซต เป็นหัวข้อหนึ่งจากบทเรียนเรื่อง เซต ในวิชาคณิตศาสตร์ ม.4 ซึ่งจะมีนิยาม และสมบัติของมัน เราลองมาเรียนกันครับว่าสับเซตและเพาเวอร์เซตเป็นอย่างไร
สับเซต (Subset)
ถ้าสมาชิกทุกตัวของ A เป็นสมาชิกของ B แล้ว จะเรียกว่า A เป็นสับเซตของ B จะเขียนว่า
เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B
เซต A เป็นสับเซตของเซต B แทนด้วย A ⊂ B
ถ้าสมาชิกบางตัวของ A ไม่เป็นสมาชิกของ B จะเรียกว่า A ไม่เป็นสับเซตของ B
เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B
เซต A ไม่เป็นสับเซตของเซต B แทนด้วย A ⊄ B
สมบัติของสับเซต
1) A ⊂ A (เซตทุกเซตเป็นสับเซตของตัวมันเอง)
2) A ⊂ U (เซตทุกเซตเป็นสับเซตของเอกภพสัมพัทธ์)
3) ø ⊂ A (เซตว่างเป็นสับเซตของทุกๆ เซต)
4) ถ้า A ⊂ ø แล้ว A = ø
5) ถ้า A ⊂ B และ B ⊂ C แล้ว A ⊂ C (สมบัติการถ่ายทอด)
6) A = B ก็ต่อเมื่อ A ⊂ B และ B ⊂ A
7) ถ้า A มีจำนวนสมาชิก n ตัว สับเซตของเซตจะมีทั้งสิ้น 2n สับเซต
สับเซตแท้
นิยาม A เป็นสับเซตแท้ของ B ก็ต่อเมื่อ A⊂B และ A ≠ B
ตัวอย่าง กำหนดให้ A = { a , b , c } จงหาสับเซตแท้ทั้งหมดของ A
วิธีทำ สับเซตแท้ของ A ได้แก่
ø, {a} , {b} ,{c} , {a,b} , {a ,c} , {b,c}
มีจำนวนสมาชิกทั้งสิ้น 7 สับเซต
หมายเหตุ ถ้า A มีจำนวนสมาชิก n ตัว สับเซตแท้ของเซตA จะมีทั้งสิ้น 2n –1 สับเซต
เพาเวอร์เซต (Power Set)
คำว่า เพาเวอร์เซต เป็นคำศัพท์เฉพาะ ซึ่งใช้เป็นชื่อเรียกเซตเซตหนึ่งที่เกี่ยวข้องกับเรื่องสับเซต
เพาเวอร์เซตของ A เขียนแทนด้วย P(A)
P(A) คือเซตที่มีสับเซตทั้งหมดของ A เป็นสมาชิก
สมบัติของเพาเวอร์เซต
ให้ A , B เป็นเซตใดๆ
1) ø ⊂ P(A)
2) A ⊂ P(A)
3) P(A) ≠ ø
4) P(A) ⊂ P(B) ก็ต่อเมื่อ A ⊂ B
5) ถ้า A มีสมาชิก n ตัว P(A) จะมีสมาชิก 2n ตัว
แผนภาพเวนน์-ออยเลอร์ (เซต) คณิตศาสตร์ ม.4 มีความสำคัญมากในการแก้ปัญหาเกี่ยวกับโจทย์ปัญหาของเซต เน้นที่การหาจำนวนสมาชิกของเซตภายใต้เงื่อนไขที่กำหนดให้ ซึ่งเราสามารถแก้ปัญหาการหาจำนวนสมาชิกของเซตโดยทั่วไป
แผนภาพออยเลอร์ (Euler diagram)
แผนภาพออยเลอร์ (Euler diagram) เป็นแผนภาพที่ใช้ในการอธิบายความสัมพันธ์ของเซตต่าง ๆ โดยให้วงกลมแต่ละวงแทนแต่ละเซต และแสดงความสัมพันธ์ของแต่ละเซตด้วย การครอบซึ่งแสดงความเป็นสับเซต การทับซ้อนกัน หรือการไม่ทับซ้อนกันซึ่งแสดงว่าทั้งสองเซตไม่มีความสัมพันธ์กัน ลักษณะแผนภาพวงกลมเช่นนี้เชื่อว่าถูกใช้ครั้งแรกโดยนักคณิตศาสตร์ชาวสวิสนามว่า เลออนฮาร์ด ออยเลอร์ แผนภาพออยเลอร์นั้นมียังลักษณะคล้ายคลึงกันกับแผนภาพเวนน์มาก ในทฤษฎีเซตซึ่งเป็นแขนงหนึ่งของคณิตศาสตร์จึงนิยมใช้แผนภาพประยุกต์จากแผนภาพทั้งสองในการอธิบายเซตต่าง ๆ ให้เข้าใจได้ง่ายยิ่งขึ้น
แผนภาพเวนน์-ออยเลอร์ (Venn-Euler diagram)
แผนภาพเวนน์-ออยเลอร์ เป็นแผนภาพแสดงความเกี่ยวข้องของเซตต่าง ๆ ซึ่งชื่อที่ใช้เรียกเป็นชื่อของนักคณิตศาสตร์สองคน คือ จอห์น เวนน์ และ เลโอนาร์ด ออยเลอร์
การเขียนแผนภาพเวนน์-ออยเลอร์
การเขียนแผนภาพเวนน์-ออยเลอร์ มักเขียนแทนเอกภพสัมพัทธ์ U ด้วยสี่เหลี่ยมผืนผ้าหรือรูปปิดใด ๆ ส่วนเซต A,B,C,D,… ซึ่งเป็นเซตย่อยของ U อาจเขียนแทนด้วยวงกลมหรือวงรีหรือรูปปิดใด ๆ โดยให้ภาพทื่แทนเซตย่อยอยู่ในรูปสี่เหลี่ยมผืนผ้าที่แทนเอกภพสัมพัทธ์
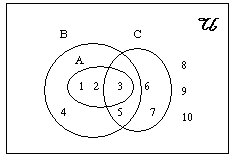
ถ้ากำหนดให้ U = {1,2,3,4,5,6,7,8,9,10}
A = {1,2,3} , B = {1,2,3,4,5} , C = {3,5,6,7}
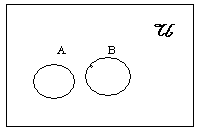
ถ้าเซต A และ B ไม่มีสมาชิกร่วมกันแผนภาพมีลักษณะดังนี้
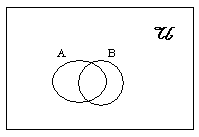
ถ้าเซต A และ B มีสมาชิกร่วมกันบางส่วน ( ไม่ทั้งหมด ) แผนภาพมีลักษณะดังนี้
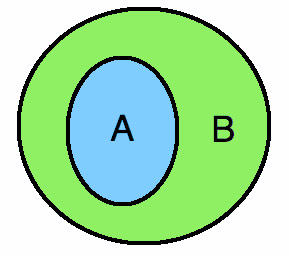
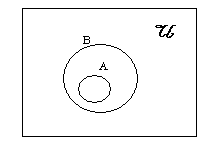
ถ้า A ⊂ B แต่ A ≠B แผนภาพจะมีลักษณะดังนี้
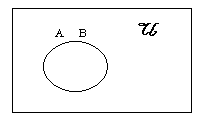
ถ้า A=B แผนภาพมีลักษณะดังนี้
ที่มา : http://www.tewfree.com/
ขอบคุณมากๆครับ เป็นความรู้อย่างมาก
ตอบลบแล้วแบบฝึกหัดละครับ
ตอบลบ